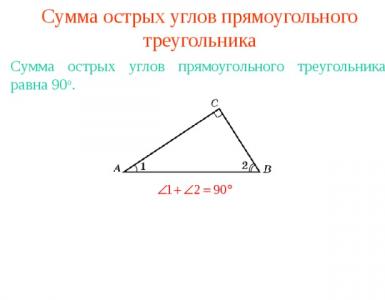
Дискретные случайные величины. Понятие случайной величины
Случайная величина называется дискретной, если совокупность всех ее возможных значений представляет собой конечное или бесконечное, но обязательно счетное множество значений, т.е. такое множество, все элементы которого могут быть (по крайней мере, теоретически) пронумерованы и выписаны в соответствующей последовательности.
Такие из перечисленных выше случайных величин, как количество очков, выпадающих при бросании игрального кубика, число посетителей аптеки в течение дня, количество яблок на дереве являются дискретными случайными величинами.
Наиболее полную информацию о дискретной случайной величине дает закон распределения этой величины – это соответствие между всеми возможными значениями этой случайной величины и соответствующими им вероятностями.
Закон распределения дискретной случайной величины часто задают в виде двухстрочной таблицы, в первой строке которой перечислены все возможные значения этой величины (в порядке возрастания), а во второй -соответствующие этим значениям вероятности:
| X | х 1 | х 2 | … | х n |
| P | р 1 | р 2 | … | р n |
Так как все возможные значения дискретной случайной величины представляют полную систему, то сумма вероятностей равна единице (условие нормировки):
Пример 4. Имеется десять студенческих групп, насчитывающих соответственно 12, 10, 8, 10, 9, 12, 8, 11,10 и 9 студентов. Составить закон распределения случайной величины X, определяемой как число студентов в наугад выбранной группе.
Решение . Возможными значениями рассматриваемой случайной величины X (в порядке возрастания) являются 8, 9, 10, 11, 12. Вероятность того, что в наугад выбранной группе окажется 8 студентов, равна
Аналогично можно найти вероятности остальных значений случайной величины X:
Таким образом, искомый закон распределения:
| X | |||||
| P | 0,2 | 0,2 | 0,3 | 0,1 | 0,2 |
Закон распределения дискретной случайной величины можно задать также с помощью формулы, позволяющей для каждого возможного значения этой величины определить соответствующую вероятность (например, распределение Бернулли, распределение Пуассона). Для описания определенных особенностей дискретной случайной величины используют ее основные числовые характеристики : математическое ожидание, дисперсию и среднее квадратическое отклонение (стандарт).
Математическим ожиданием М (X) (используется также обозначение «μ») дискретной случайной величины х называется сумма произведений каждого из всех ее возможных значений на соответствующие вероятности:
Основной смысл математического ожидания дискретной случайной величины состоит в том, что оно представляет собой среднее значение данной величины. Другими словами, если произведено некоторое количество испытаний, по результатам которых найдено среднее арифметическое всех наблюдавшихся значений дискретной случайной величины X, то это среднее арифметическое приближенно равно (тем точнее, чем больше количество испытаний) математическому ожиданию данной случайной величины.
Приведем некоторые свойства математического ожидания.
1. Математическое ожидание постоянной величины равно этой постоянной величине:
М(С)=С
2. Математическое ожидание произведения постоянного множителя на дискретную случайную величину равно произведению этого постоянного множителя на математическое ожидание данной случайной величины:
М(kX)=kM(X)
3. Математическое ожидание суммы двух случайных величин равно сумме математических ожиданий этих величин:
M(X+Y)=M(X)+M(Y)
4. Математическое ожидание произведения независимых случайных величин равно произведению их математических ожиданий:
M(X·Y)=M(X)·M(Y)
Отдельные значения дискретной случайной величины группируются около математического ожидания как центра. Для характеристики степени разброса возможных значений дискретной случайной величины относительно ее математического ожидания вводят понятие дисперсии дискретной случайной величины.
Дисперсией D(X) (используется также обозначение «σ 2 ») дискретной случайной величины X называется математическое ожидание квадрата отклонения этой величины от ее математического ожидания:
D(X)=σ 2 =М((X - μ) 2), (11)
На практике дисперсию удобнее вычислить по формуле
D(X)=σ 2 =М(X 2) - μ 2 , (12)
Перечислим основные свойства дисперсии.
- Дисперсия постоянной величины равна нулю:
- Дисперсия любой случайной величины есть число неотрицательное:
D(X)≥0
- Дисперсия произведения постоянного множителя k на дискретную случайную величину равна произведению квадрата этого постоянного множителя на дисперсию данной случайной величины:
D(kX)=k 2 ·D(X).
В вычислительном отношении более удобна не дисперсия, а другая мера рассеивания случайной величины X , которая чаще всего и используется – среднее квадратическое отклонение (стандартное отклонение или просто стандарт ).
Средним квадратическим отклонением дискретной случайной величины называется квадратный корень из ее дисперсии:
Удобство стандартного отклонения состоит в том, что оно имеет размерность самой случайной величины X , в то время как дисперсия имеет размерность, представляющую квадрат размерности X.
Конец работы -
Эта тема принадлежит разделу:
Элементы теории вероятностей
Научно методическое обоснование темы.. теория вероятностей изучает закономерности проявляющиеся при изучении таких.. многие случайные события могут быть количественно оценены случайными величинами которые принимают значения в..
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ:
Что будем делать с полученным материалом:
Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:
ОДНОМЕРНЫЕ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
Понятие случайной величины. Дискретные и непрерывные случайные величины. Функция распределения вероятностей и ее свойства. Плотность распределения вероятности и ее свойства. Числовые характеристики случайных величин: математическое ожидание, дисперсия и их свойства, среднее квадратическое отклонение, мода и медиана; начальные и центральные моменты, асимметрия и эксцесс.
1. Понятие случайной величины.
Случайной называется величина, которая принимает в результате испытаний то или иное (но при этом только одно) возможное значение, заранее известное, меняющееся от испытания к испытанию и зависящее от случайных обстоятельств. В отличие от случайного события, являющегося качественной характеристикой случайного результата испытания, случайная величина характеризует результат испытания количественно. Примерами случайной величины могут служить размер обрабатываемой детали, погрешность результата измерения какого-либо параметра изделия или среды. Среди случайных величин, с которыми приходится встречаться на практике, можно выделить два основных типа: дискретные величины и непрерывные.
Дискретной называется такая случайная величина, которая принимает конечное или бесконечное счетное множество значений. Например, частота попаданий при трех выстрелах; число дефектных изделий в партии из штук; число вызовов, поступающих на телефонную станцию в течение суток; число отказов элементов прибора за определенный промежуток времени при испытании его на надежность; число выстрелов до первого попадания в цель и т. д.
Непрерывной называется такая случайная величина, которая может принимать любые значения из некоторого конечного или бесконечного интервала. Очевидно, число возможных значений непрерывной случайной величины бесконечно. Например, ошибка при измерении дальности радиолокатора; время безотказной работы микросхемы; погрешность изготовления деталей; концентрация соли в морской воде и т. д.
Случайные величины обычно обозначают буквами ,и т. д., а их возможные значения -,и т. д. Для задания случайной величины недостаточно перечислить все ее возможные значения. Необходимо также знать, как часто могут появиться те или иные ее значения в результате испытаний при одних и тех же условиях, т. е. нужно задать вероятности их появления. Совокупность всех возможных значений случайной величины и соответствующих им вероятностей составляет распределение случайной величины.
2. Законы распределения случайной величины.
Законом распределения случайной величины называется всякое соответствие между возможными значениями случайной величины и соответствующими им вероятностями. Про случайную величину говорят, что она подчиняется данному закону распределения. Две случайные величины называются независимыми , если закон распределения одной из них не зависит то того, какие возможные значения приняла другая величина. В противном случае случайные величины называются зависимыми . Несколько случайных величин называются взаимно независимыми , если законы распределения любого числа из них не зависит от того, какие возможные значения приняли остальные величины.
Закон распределения случайной величины может быть задан в виде таблицы, в виде функции распределения, в виде плотности распределения. Таблица, содержащая возможные значения случайной величины и соответствующие вероятности, является простейшей формой задания закона распределения случайной величины:
Табличное задание закона распределения может быть использовано только для дискретной случайной величины с конечным числом возможных значений. Табличная форма задания закона случайной величины называется также рядом распределения.
Для наглядности ряд распределения представляют графически. При графическом изображении в прямоугольной системе координат по оси абсцисс откладывают все возможные значения случайной величины, а по оси ординат - соответствующие вероятности. Затем строят точки и соединяют их прямолинейными отрезками. Полученная фигура называетсямногоугольником распределения (рис. 5). Следует помнить, что соединение вершин ординат делается только в целях наглядности, так как в промежутках между и,и, и т. д. случайная величиназначений принять не может, поэтому вероятности ее появления в этих промежутках равны нулю.
Многоугольник распределения, как и ряд распределения, является одной из форм задания закона распределения дискретной случайной величины. Они могут иметь самую различную форму, однако все обладают одним общим свойством: сумма ординат вершин многоугольника распределения, представляющая собой сумму вероятностей всех возможных значений случайной величины, всегда равна единице. Это свойство вытекает из того, что все возможные значения случайной величины образуют полную группу несовместных событий, сумма вероятностей которых равна единице.
Дискретная случайная величина и закон ее распределения
Наряду с понятием случайного события в теории вероятности используется и более удобное понятие случайной величины .
Определение. Случайной величиной называется величина, принимающая в результате опыта одно из своих возможных значений, причем заранее неизвестно, какое именно.
Будем обозначать случайные величины заглавными буквами латинского алфавита (Х, Y, Z,… ), а их возможные значения – соответствующими малыми буквами (x i , y i ,… ).
Примеры: число очков, выпавших при броске игральной кости; число появлений герба при 10 бросках монеты; число выстрелов до первого попадания в цель; расстояние от центра мишени до пробоины при попадании.
Можно заметить, что множество возможных значений для перечисленных случайных величин имеет разный вид: для первых двух величин оно конечно (соответственно 6 и 11 значений), для третьей величины множество значений бесконечно и представляет собой множество натуральных чисел, а для четвертой – все точки отрезка, длина которого равна радиусу мишени. Таким образом, для первых трех величин получаем множество значений из отдельных (дискретных), изолированных друг от друга значений, а для четвертой оно представляет собой непрерывную область. По этому показателю случайные величины подразделяются на две группы: дискретные и непрерывные.
Определение. дискретной , если она принимает отдельные, изолированные возможные значения с определенными вероятностями. Число возможных значений дискретной случайной величины может быть конечным или бесконечным.
Определение. Случайная величина называется непрерывной , если множество ее возможных значений целиком заполняет некоторый конечный или бесконечный промежуток. Число возможных значений непрерывной случайной величины бесконечно.
Для задания дискретной случайной величины нужно знать ее возможные значения и вероятности, с которыми принимаются эти значения. Соответствие между ними называется законом распределения случайной величины. Он может иметь вид таблицы, формулы или графика.
Таблица, в которой перечислены возможные значения дискретной случайной величины и соответствующие им вероятности, называется рядом распределения :
| x i | x 1 | x 2 | … | x n | … | возможные значения |
| p i | p 1 | p 2 | … | p n | … | вероятность возможных значений |
Заметим, что событие, заключающееся в том, что случайная величина примет одно из своих возможных значений, является достоверным, поэтому или
Задача. Монету бросают 5 раз. Случайная величина X – количество выпадения герба. Составить ряд распределения случайной величины Х.
Решение. Очевидно, что Х может принимать 5 значений: 0, 1, 2, 3, 4, 5, то есть X = 0, 1, 2, 3, 4, 5. По условию , . Вычислим вероятность каждого значения по формуле Бернулли: .
Герб не выпадет ни разу (k = 0) : .
Или .
Герб выпадет один раз (k = 1)
:
.
Герб выпадет два раза (k = 2) :
Герб выпадет три раза (k = 3) :
Герб выпадет четыре раза (k = 4) :
Герб выпадет пять раз (k = 5) :
Следовательно, ряд распределения имеет вид:
| биномиальные вероятности |
При этом сумма вероятностей равна единице:
Графически закон распределения дискретной случайной величины можно представить в виде многоугольника распределения – ломаной, соединяющей точки плоскости с координатами (x i , p i ). То есть по оси абсцисс откладываются возможные значения случайной величины, а по оси ординат – вероятности этих значений. Для наглядности полученные точки соединяются отрезками прямых. Многоугольник распределения, так же как и ряд распределения, полностью характеризует случайную величину и является одной из форм закона распределения.
Отправить свою хорошую работу в базу знаний просто. Используйте форму, расположенную ниже
Студенты, аспиранты, молодые ученые, использующие базу знаний в своей учебе и работе, будут вам очень благодарны.
Размещено на http://www.allbest.ru/
Дискретные случайные величины
Пусть производится некоторое испытание, результатом которого является одно из несовместных случайных событий (число событий или конечно или счетно, то есть события можно пронумеровать). Каждому исходу поставлено в соответствие некоторое действительное число, то есть на множестве случайных событий задана действительная функция Х со значениями. Эта функция Х называется дискретной случайной величиной (термин «дискретная» используется потому, что значения случайной величины - это отдельные числа, в отличии от непрерывных функций). Поскольку значения случайной величины изменяются в зависимости от случайных событий, то основной интерес представляют вероятности, с которыми случайная величина принимает различные числовые значения. Законом распределения случайной величины называется всякое соотношение, устанавливающее связь между возможными значениями случайной величины и соответствующими им вероятностями. Закон распределения может иметь различные формы. Для дискретной случайной величины законом распределения является совокупность пар чисел (), где - возможные значения случайной величины, а - вероятности, с которыми она принимает эти значения: . При этом.
Пары можно рассматривать, как точки в некоторой системе координат. Соединив эти точки отрезками прямых, мы получим графическое изображение закона распределения - многоугольник распределения. Чаще всего закон распределения дискретной случайной величины записывается в виде таблицы, в которую внесены пары.
Пример. Монета подброшена два раза. Составить закон распределения числа выпадения «гербов» в данном испытании.
Решение. Случайная величина Х - число выпадений «герба» в данном испытании. Очевидно, что Х может принимать одно из трех значений: 0, 1, 2. Вероятность появления «герба» при одном подбрасывании монеты равна р=0,5, а выпадения «решки» q = 1 - p = 0,5. Вероятности, с которыми случайная величина принимает перечисленные значения, найдем по формуле Бернулли:
Закон распределения случайной величины Х запишем в виде таблицы распределения
Контроль:
Некоторые законы распределения дискретных случайных величин, часто встречающиеся при решении различных задач, получили специальные названия: геометрическое распределение, гипергеометрическое распределение, биномиальное распределение, распределение Пуассона и другие.
Закон распределения дискретной случайной величины может быть задан с помощью функции распределения F(x), которая равна вероятности того, что случайная величина Х будет принимать значения на промежутке????х?: F(x) = P(X Функция F(х) определена на всей действительной оси и обладает следующими свойствами: 1) ? ? F(х) ? 1; 2) F(х) - неубывающая функция; 3) F(??) = 0, F(+?) = 1; 4) F(b) - F(a) = P(a ? X < b) - вероятность того, что случайная величина Х примет значения на промежутке 2 =(1-2.3) 2 =1.69 2 =(2-2.3) 2 =0.09 2 =(5-2.3) 2 =7.29 Напишем закон распределения квадрата отклонения: Решение: Найдем математическое ожидание М(х): M(x)=2*0.1+3*0.6+5*0.3=3.5 Напишем закон распределения случайной величины X 2 Найдем математическое ожидание M(x 2): M(x 2)=4*0.1+9*0.6+25*0.3=13.5 Искомая дисперсия D(x)=M(x 2)- 2 =13.3-(3.5) 2 =1.05 Свойства дисперсии 1. Дисперсия постоянной величины С равна нулю: D(C)=0 2. Постоянный множитель можно выносить за знак дисперсии, возводя его в квадрат. D(Cx)=C 2 D(x) 3. Дисперсия суммы независимых случайных величин равна сумме дисперсий этих величин. D(X 1 +X 2 +...+X n)=D(X 1)+D(X 2)+...+D(X n) 4. Дисперсия биномиального распределения равна произведению числа испытаний на вероятности появления и непоявления события в одном испытании D(X)=npq. Для оценки рассеяния возможных значений случайной величины вокруг ее среднего значения кроме дисперсии служат и некоторые другие характеристики. К их числу относится среднее квадратичное отклонение. ОПРЕДЕЛЕНИЕ. Средним квадратичным отклонением случайной величины Х называют квадратный корень из дисперсии: Пример 8. Случайная величина Х задана законом распределения Найти среднее квадратичное отклонение у(x) Решение: Найдем математическое ожидание Х: M(x)=2*0.1+3*0.4+10*0.5=6.4 Найдем математическое ожидание X 2: M(x 2)=2 2 *0.1+3 2 *0.4+10 2 *0.5=54 Найдем дисперсию: D(x)=M(x 2)=M(x 2)- 2 =54-6.4 2 =13.04 Искомое среднее квадратичное отклонение у(X)=vD(X)=v13.04?3.61 Теорема. Среднее квадратичное отклонение суммы конечного числа взаимно независимых случайных величин равно квадратному корню из суммы квадратов средних квадратичных отклонений этих величин: Случайные величины Понятие случайной величины является основным в теории вероятностей и ее приложениях. Случайными величинами, например, являются число выпавших очков при однократном бросании игральной кости, число распавшихся атомов радия за данный промежуток времени, число вызовов на телефонной станции за некоторый промежуток времени, отклонение от номинала некоторого размера детали при правильно налаженном технологическом процессе и т. д. Таким образом, случайной
величиной
называется переменная величина, которая в результате опыта может принимать то или иное числовое значение. В дальнейшем мы рассмотрим два типа случайных величин -- дискретные и непрерывные. 1. Дискретные случайные величины Рассмотрим случайную величину * , возможные значения которой образуют конечную или бесконечную последовательность чисел x
1
,
x
2
,
.
..,
x
n
,
.
..
.
Пусть задана функция p(x)
, значение которой в каждой точке x=x
i
(i=1,2,
.
..)
равно вероятности того, что величина примет значение x
i
.
Такая случайная величина называется дискретной
(прерывной)
. Функция р(х)
называется законом
распределения
вероятностей
случайной
величины
, или кратко, законом
распределения
. Эта функция определена в точках последовательности x
1
,
x
2
,
.
..,
x
n
,
.
..
.
Так как в каждом из испытаний случайная величина принимает всегда какое-либо значение из области ее изменения, то Пример
1.
Случайная величина -- число очков, выпадающих при однократном бросании игральной кости. Возможные значения -- числа 1, 2, 3, 4, 5 и 6. При этом вероятность того, что примет любое из этих значений, одна и та же и равна 1/6. Какой будет закон распределения? (Решение
) Пример
2.
Пусть случайная величина - число наступления события A
при одном испытании, причем P(A)=p
. Множество возможных значений состоит из 2-х чисел 0 и 1: =0
, если событие A
не произошло, и =1
, если событие A
произошло. Таким образом, Предположим, что производится n
независимых испытаний, в результате каждого из которых может наступить или не наступить событие A
. Пусть вероятность наступления события A
при каждом испытании равна p
A
при n
независимых испытаниях. Область изменения состоит из всех целых чисел от 0
до n
включительно. Закон распределения вероятностей р(m)
определяется формулой Бернулли (13"): Закон распределения вероятностей по формуле Бернулли часто называют биномиальным
, так как P
n
(m)
представляет собой m
-й член разложения бинома. Пусть случайная величина может принимать любое целое неотрицательное значение, причем где -- некоторая положительная постоянная. В этом случае говорят, что случайная величина распределена по закону
Пуассона
, Заметим, что при k=0
следует положить 0!=1
. Как мы знаем, при больших значениях числа n
независимых испытаний вероятность P
n
(m)
наступления m
раз события A
удобнее находить не по формуле Бернулли, а по формуле Лапласа [см. формулу (15)]. Однако последняя дает большие погрешности при малой вероятности р
появления события А
в одном испытании. В этом случае для подсчета вероятности P
n
(m)
удобно пользоваться формулой Пуассона, в которой следует положить. Формулу Пуассона можно получить как предельный случай формулы Бернулли при неограниченном увеличении числа испытаний n
и при стремлении к нулю вероятности. Пример
3.
На завод прибыла партия деталей в количестве 1000 шт. Вероятность того, что деталь окажется бракованной, равна 0,001. Какова вероятность того, что среди прибывших деталей будет 5 бракованных? (Решение
) Распределение Пуассона часто встречается и в других задачах. Так, например, если телефонистка в среднем за один час получает N
вызовов, то, как можно показать, вероятность Р(k)
того, что в течение одной минуты она получит k
вызовов, выражается формулой Пуассона, если положить. Если возможные значения случайной величины образуют конечную последовательность x
1
,
x
2
,
.
..,
x
n
, то закон распределения вероятностей случайной величины задают в виде следующей таблицы, в которой Значения Вероятности p(xi)
Эту таблицу называют рядом
распределения
случайной величины. Наглядно функцию р(х)
можно изобразить в виде графика. Для этого возьмем прямоугольную систему координат на плоскости. По горизонтальной оси будем откладывать возможные значения случайной величины, а по вертикальной оси - значения функции. График функции р(х)
изображен на рис. 2. Если соединить точки этого графика прямолинейными отрезками, то получится фигура, которая называется многоугольником
распределения
. Пример
4.
Пусть событие А
-- появление одного очка при бросании игральной кости; Р(A)=1/6
. Рассмотрим случайную величину -- число наступлений события А
при десяти бросаниях игральной кости. Значения функциир(х)
(закона распределения) приведены в следующей таблице: Значения Вероятности p(xi)
Вероятности p(x
i
)
вычислены по формуле Бернулли при n=10
. Для x>6
они практически равны нулю. График функции p(x) изображен на рис. 3. Функция распределения вероятностей случайной величины и ее свойства Рассмотрим функцию F(х)
, определенную на всей числовой оси следующим образом: для каждого х
значениеF(х)
равно вероятности того, что дискретная случайная величина примет значение, меньшее х
, т. е. Эта функция называется функцией
распределения
вероятностей
, или кратко, функцией
распределения
. Пример
1.
Найти функцию распределения случайной величины, приведенной в примере 1, п. 1. (Решение
) Пример
2.
Найти функцию распределения случайной величины, приведенной в примере 2, п. 1. (Решение
) Зная функцию распределения F(x)
, легко найти вероятность того, что случайная величина удовлетворяет неравенствам. Рассмотрим событие, заключающееся в том, что случайняя величина примет значение, меньшее. Это событие распадается на сумму двух несовместных событий: 1) случайная величина принимает значения, меньшие, т.е. ; 2) случайная величина принимает значения, удовлетворяющие неравенствам. Используя аксиому сложения, получаем Но по определению функции распределения F(x)
[см. формулу (18)], имеем cледовательно, Таким образом, вероятность
попадания
дискретной
случайной
величины
в
интервал
равна
приращению
функции
распределения
на
этом
интервале.
Рассмотрим
основные
свойства
функции
распределения.
1°. Функция
распределения
является
неубывающей.
В самом деле, пусть < . Так как вероятность любого события неотрицательна, то. Поэтому из формулы (19) следует, что 2°. Значения
функции
распределения
удовлетворяют
неравенствам
. Это свойство вытекает из того, что F(x)
определяется как вероятность [см. формулу (18)]. Ясно, что * и. 3°. Вероятность
того,
что
дискретная
случайная
величина
примет
одно
из
возможных
значений
x
i
,
равна
скачку
функции
распределения
в
точке
x
i
. Действительно, пусть x
i
- значение, принимаемое дискретной случайной величиной, и. Полагая в формуле (19) , получим В пределе при вместо вероятности попадания случайной величины на интервал получим вероятность того, что величина примет данное значение x
i
: C другой стороны, получаем, т.е. предел функции F(x)
справа, так как. Следовательно, в пределе формула (20) примет вид т.е. значение p(x
i
)
равно скачку функции ** x
i
. Это свойство наглядно иллюстрируется на рис. 4 и рис. 5. Непрерывные случайные величины Кроме дискретных случайных величин, возможные значения которых образуют конечную или бесконечную последовательность чисел, не заполняющих сплошь никакого интервала, часто встречаются случайные величины, возможные значения которых образуют некоторый интервал. Примером такой случайной величины может служить отклонение от номинала некоторого размера детали при правильно налаженном технологическом процессе. Такого рода, случайные величины не могут быть заданы с помощью закона распределения вероятностей р(х)
. Однако их можно задать с помощью функции распределения вероятностей F(х)
. Эта функция определяется точно так же, как и в случае дискретной случайной величины: Таким образом, и здесь функция F(х)
определена на всей числовой оси, и ее значение в точке х
равно вероятности того, что случайная величина примет значение, меньшее чем х
. Формула (19) и свойства 1° и 2° справедливы для функции распределения любой случайной величины. Доказательство проводится аналогично случаю дискретной величины. Случайная величина называется непрерывной
, если для нее существует неотрицательная кусочно-непрерывная функция* , удовлетворяющая для любых значений x
равенству Функция называется плотностью
распределения
вероятностей
, или кратко, плотностью
распределения
. Если x
1
Исходя из геометрического смысла интеграла как площади, можно сказать, что вероятность выполнения неравенств равна площади криволинейной трапеции с основанием
, ограниченной сверху кривой (рис. 6). Так как, а на основании формулы (22) Пользуясь формулой (22), найдем как производную интеграла по переменной верхней границе, считая плотность распределения непрерывной**: Заметим, что для непрерывной случайной величины функция распределения F(х)
непрерывна в любой точке х
, где функция непрерывна. Это следует из того, что F(х)
в этих точках дифференцируема. На основании формулы (23), полагая x
1
=x
, имеем В силу непрерывности функции F(х)
получим, что Следовательно Таким образом, вероятность
того,
что
непрерывная
случайная
величина
может
принять
любое
отдельное
значение
х,
равна
нулю
. Отсюда следует, что события, заключающиеся в выполнении каждого из неравенств Имеют одинаковую вероятность, т.е. В самом деле, например, Замечание.
Как мы знаем, если событие невозможно, то вероятность его наступления равна нулю. При классическом определении вероятности, когда число исходов испытания конечно, имеет место и обратное предложение: если вероятность события равна нулю, то событие невозможно, так как в этом случае ему не благоприятствует ни один из исходов испытания. В случае непрерывной случайной величины число возможных ее значений бесконечно. Вероятность того, что эта величина примет какое-либо конкретное значение x
1
как мы видели, равна нулю. Однако отсюда не следует, что это событие невозможно, так как в результате испытания случайная величина может, в частности, принять значение x
1
. Поэтому в случае непрерывной случайной величины имеет смысл говорить о вероятности попадания случайной величины в интервал, а не о вероятности того, что она примет какое-то конкретное значение. Так, например, при изготовлении валика нас не интересует вероятность того, что его диаметр будет равен номиналу. Для нас важна вероятность того, что диаметр валика не выходит из поля допуска. Пример.
Плотность распределения непрерывной случайной величины задана следующим образом: График функции представлен па рис. 7. Определить вероятность того, что случайная величина примет значение, удовлетворяющее неравенствам.Найти функцию распределения заданной случайной величины. (Решение
) Следующие два пункта посвящены часто встречающимся на практике распределениям непрерывных случайных величин -- равномерному и нормальному распределениям. * Функция называется кусочно-непрерывной на всей числовой оси, если она на любом сегменте или непрерывна, или имеет конечное число точек разрыва I рода. ** Правило дифференцирования интеграла с переменной верхней границей, выведенное в случае конечной нижней границы, остается справедливым и для интегралов с бесконечной нижней границей. В самом деле, Так как интеграл есть величина постоянная. Случайные величины Под случайными величинами понимают числовые характеристики случайных событий. Другими словами, случайные величины - это числовые результаты экспериментов, значения которых которые невозможно (в данное время) предсказать заранее. Например, следующие величины можно рассматривать как случайные: 2. Процент мальчиков среди детей, родившихся в заданном роддоме в некоторый определенный день. 3. Число и площадь пятен на Солнце, видимых в некоторой обсерватории в течение определенного дня. 4. Число студентов, опоздавших на данную лекцию. 5. Курс доллара на бирже (скажем, на ММВБ), хотя может быть он и не так уж “случаен”, как это кажется обывателям. 6. Число отказов оборудования в заданный день на определенном предприятии. Случайные величины делят на дискретные и непрерывные в зависимости от того, каково множество всех возможных значений соответствующей характеристики - дискретное или же непрерывное. Это деление довольно условно, но полезно при выборе адекватных методов исследования. Если число возможных значений случайной величины конечно или сопоставимо с множеством всех натуральных чисел (т.е. может быть перенумеровано), то случайную величину PDF created with FinePrint pdfFactory trial version http://www.fineprint.com называют дискретной. В противном случае ее называют непрерывной, хотя на самом деле как бы неявно предполагается, что фактически непрерывные случайные величины принимают свои значение в некотором простом числовом помежутке (отрезке, интервале). Например, дискретными будут случайные величины, приведенные выше под номерами 4 и 6, а непрерывными - под номерами 1 и 3 (площади пятен). Иногда случайная величина имеет смешанный характер. Таков, например, курс доллара (или какой-то другой валюты), который фактически принимает лишь дискретный набор значений, но при этом оказывается удобным считать, что множество его значений «непрерывно». Случайные величины можно задавать разными способами. Дискретные случайные величины обычно задаются своим законом распределения. Тут каждому возможному значению x1, x2,... случайной величины X сопоставляется вероятность p1,p2,... этого значения. В результате образуется таблица, состоящая из двух строк: Это и есть закон распределения случайной величины. Непрерывные случайные величины законом распределения задать невозможно, так как по самому своему определению их значения невозможно перенумеровать и потому задание в виде таблицы тут исключается. Однако для непрерывных случайных величин есть другой способ задания (применимый, кстати, и для дискретных величин) - это функция распределения: равная вероятности события , которое состоит в том, что случайная величина X примет значение, меньшее заданного числа x. Часто вместо функции распределения удобно использовать другую функцию - плотность f(x) распределения случайной величины X. Ее еще иногда называют дифференциальной функцией распределения, а F(x) в этой терминологии называется интегральной функцией распределния. Эти две функции взаимно определяют друг друга по следующим формулам: Если случайная величина дискретна, то для нее понятие функции распределения тоже имеет смысл, в этом случай график функции распределения состоит из горизонтальных участков, каждый из которых расположен выше предыдущего на величину, равную pi. Важными примерами дискретных величин являются, например, биномиально распределенные величины (распределение Бернулли), для которых PDF created with FinePrint pdfFactory trial version http://www.fineprint.com n pk(1-p)n-k= !()! где p - вероятность отдельного события (ее иногда условно называют “вероятностью успеха”). Так распределены результаты серии последовательных однородных испытаний (схема Бернулли). Предельным случаем биномиального распределения (при увеличении числа испытаний) является распределение Пуассона, для которого pk=?k/k!·exp(-?), где?>0 некоторый положительный параметр. Простейший пример непрерывного распределения - равномерное распределение. Оно на отрезке имеет постоянную плотность распределения, равную 1/(b-a), а вне этого отрезка плотность равна 0. Чрезвычайно важным примером непрерывного распределения является нормальное распределение. Оно задается двумя параметрами m и? (математическим ожиданием и среднеквадратичным отклонением - см. ниже), его плотность распределения имеет вид: 1 exp(-(x-m)2/2?2) Фундаментальная роль нормального распределения в теории вероятностей объясняется тем, что в силу Центральной Предельной Теоремы (ЦПТ) сумма большого числа случайных величин, которые являются попарно независимыми (о понятии независимости случайных величин см. ниже) или слабо зависимыми, оказывается приближенно распределенной по нормальному закону. Отсюда следует, что случайная величина, случайность которой вызвана наложением большого числа слабо зависимых между собой случайных факторов, может рассматриваться приближенно как распределенная нормально (в независимости от того, как были распределены слагающие ее факторы). Другими словами - нормальный закон распределения весьма универсален. Имеется несколько числовых характеристик, которые удобно использовать при изучении случайных величин. Среди них выделим математическое ожидание равное среднему значению случайной величины, дисперсию D(X)=M(X-M(X))2, равную математическому ожиданию квадрата отклонения случайной величины от среднего значения, и еще одну, удобную на практике дополнительную величину (той же размерности, что и исходная случайная величина): называемую среднеквадратичным отклонением. Будем предполагать (не оговаривая этого в дальнейшем), что все выписанные интегралы существуют (т.е. сходятся на всей числовой оси). Как известно, дисперсия и среднеквадратичное отклонение характеризуют степень рассеяния случайной величины вокруг ее среднего значения. Чем PDF created with FinePrint pdfFactory trial version http://www.fineprint.com меньше дисперсия, тем более тесно группируются значения случайной величины вокруг ее среднего значения. Например, математическое ожидание для распределение Пуассона равно?, для равномерного распределения оно равно (a+b)/2, а для нормального распределения оно равно m. Дисперсия для распределения Пуассона равна?, для равномерного распределения (b-a)2/12, а для нормального распределения равна?2. В дальнейшем будут использоваться следующие свойства математического ожидания и дисперсии: 1. M(X+Y)= M(X)+M(Y). 3. D(cX)=c2D(X), где c - произвольное постоянное число. 4. D(X+A)=D(A) для произвольной постоянной (неслучайной)величины A. Случайная величина?=U-MU называется центрированной. Из свойства 1 вытекает, что M?=M(U-MU)=M(U)-M(U)=0, то есть ее среднее значение равно 0 (с этим и связано ее название). При этом в силу свойства 4 имеем D(?)=D(U). Имеется также полезное соотношение, которое удобно использовать на практике для вычисления дисперсии и связаных с нею величин: 5. D(X)=M(X2)-M(X)2 Случайные величины X и Y называются независимыми, если для произвольных их значений x и y соответственно события и независимы. Например, независимы будут (по видимому...) результаты измерения напряжения в электросети и рост главного энергетика предприятия. А вот мощность этой электросети и зарплату главного энергетика на предприятиях уже не всегда можно считать независимыми. Если случайные величины X и Y независимы, то имеют место и следующие свойства (которые для произвольных случайных величин могут не выполняться): 5. M(XY)=M(X)M(Y). 6. D(X+Y)=D(X)+D(Y). Кроме отдельных случайных величин X,Y,... изучаются и системы случайных величин. Например, пара (X,Y) случайных величин может рассматриваться как новая случайная величина, значения которой являются двумерными векторами. Аналогично можно рассматривать и системы большего числа случайных величин, называемые многомерными случайными величинами. Такого рода системы величин тоже задаются своей функцией распределения. Например, для системы двух случайных величин эта функция имеет вид F(x,y)=P, то есть она равна вероятности события, заключающегося в том, что случайная величина X примет значение, меньшее заданного числа x, а случайная величина Y - меньшее заданного числа y. Эту функцию называют еще функцией совместного распределения случайных величин X и Y. Также можно рассматривать средний вектор - естественный аналог математического ожидания, а вот вместо дисперсии приходится изучать уже несколько числовых характеристик, называемых моментами второго порядка. Это, во-первых, две частные дисперсии DX и DY PDF created with FinePrint pdfFactory trial version http://www.fineprint.com случайных величин X и Y, рассматриваемых по-отдельности, а, во-вторых, ковариационный момент, более подробно рассмотренный ниже. Если случайные величины X и Y независимы, то F(x,y)=FX(x)FY(y) Произведение функций распределения случайных величин X и Y и потому изучение пары независимых случайных величин сводится во многом просто к изучению X и Y по отдельности. Случайные величины Выше рассматривались эксперименты, результаты которых являются случайными событиями. Однако часто возникает необходимость количественного представления результатов эксперимента в виде некоторой величины, которая называется случайной величиной. Случайная величина является вторым (после случайного события) основным объектом изучения теории вероятностей и обеспечивает более общий способ описания опыта со случайным исходом, чем совокупность случайных событий. Рассматривая эксперименты со случайным исходом, мы уже имели дело со случайными величинами. Так, число успехов в серии из испытаний - пример случайной величины. Другими примерами случайных величин являются: число вызовов на телефонной станции за единицу времени; время ожидания очередного вызова; число частиц с заданной энергией в системах частиц, рассматриваемых в статистической физике; средняя суточная температура в данной местности и т.д. Случайная величина характерна тем, что невозможно точно предсказать ее значение, которое она примет, но с другой стороны, множество ее возможных значений обычно известно. Так для числа успехов в последовательности из испытаний это множество конечно, поскольку число успехов может принимать значения. Множество значений случайной величины, может совпадать с вещественной полуосью, как в случае времени ожидания и т.д. Рассмотрим примеры экспериментов со случайным исходом, для описания которых обычно применяются случайные события и введем эквивалентное описание с помощью задания случайной величины. 1). Пусть результатом опыта может быть событие или событие. Тогда этому эксперименту можно поставить в соответствие случайную величину, которая принимает два значения, например, и с вероятностями и, причем имеют место равенства: и. Таким образом, опыт характеризуется двумя исходами ис вероятностями и, или этот же опыт характеризуется случайной величиной, принимающей два значения и с вероятностями и. 2). Рассмотрим опыт с бросанием игральной кости. Здесь исходом опыта может быть одно из событий, где - выпадение грани с номером. Вероятности,. Введем эквивалентное описание этого опыта с помощью случайной величины, которая может принимать значения с вероятностями. 3). Последовательность независимых испытаний характеризуется полной группой несовместных событий, где - событие, состоящее в появлении успехов в серии из опытов; причем вероятность события определяется формулой Бернули, т.е.. Здесь можно ввести случайную величину - число успехов, которая принимает значения с вероятностями. Таким образом, последовательность независимых испытаний характеризуется случайными событиями с их вероятностями или случайной величиной с вероятностями того, что принимает значения. 4). Однако, не для всякого опыта со случайным исходом существует столь простое соответствие между случайной величиной и совокупностью случайных событий. К примеру, рассмотрим эксперимент, в котором точка наугад бросается на отрезок. Здесь естественно ввести случайную величину - координату на отрезке, в которую попадает точка. Таким образом, можно говорить о случайном событии, где - число из. Однако вероятность этого события. Можно поступить иначе - отрезок разбить на конечное число непересекающихся отрезков и рассматривать случайные события, состоящие в том, что случайная величина принимает значения из интервала. Тогда вероятности - конечные величины. Однако и этот способ имеет существенный недостаток, поскольку отрезки выбираются произвольным образом. Для того, чтобы устранить этот недостаток рассматривают отрезки вида, где переменная. Тогда соответствующая вероятность является функцией аргумента. Это усложняет математическое описание случайной величины, но при этом описание (29.1) становится единственным, устраняется неоднозначность выбора отрезков. Для каждого из рассмотренных примеров несложно определить вероятностное пространство, где - пространство элементарных событий, - - алгебра событий (подмножеств), - вероятность, определенная для любого. Например, в последнем примере, - - алгебра всех отрезков, содержащихся в. Рассмотренные примеры приводят к следующему определению случайной величины. Пусть - вероятностное пространство. Случайной величиной называется однозначная действительная функция, определенная на, для которой множество элементарных событий вида является событием (т.е. принадлежат) для каждого действительного числа. Таким образом, в определении требуется, чтобы для каждого вещественного множество, и это условие гарантирует, что для каждого определена вероятность события. Это событие принято обозначать более краткой записью. Функция распределения вероятностей Функция называется функцией распределения вероятностей случайной величины. Функция иногда называется кратко - функция распределения, а также - интегральным законом распределения вероятностей случайной величины. Функция является полной характеристикой случайной величины, то есть представляет собой математическое описание всех свойств случайной величины и более детального способа описания этих свойств не существует. Отметим следующую важную особенность определения (30.1). Часто функцию определяют иначе: Согласно (30.1) функция является непрерывной справа. Этот вопрос подробнее будет рассмотрен ниже. Если же использовать определение (30.2), то - непрерывна слева, что является следствием применения строгого неравенства в соотношении (30.2). Функции (30.1) и (30.2) представляют собой эквивалентные описания случайной величины, поскольку не имеет значения каким определением пользоваться как при изучении теоретических вопросов, так и при решении задач. Для определенности в дальнейшем будем использовать только определение (30.1). Рассмотрим пример построения графика функции. Пусть случайная величина принимает значения, с вероятностями, причем. Таким образом, другие значения кроме указанных данная случайная величина принимает с нулевой вероятностью:, для любого,. Или как говорят, других значений кроме, случайная величина не может принимать. Пусть для определенности. Найдем значения функции для из интервалов: 1), 2), 3), 4), 5), 6), 7). На первом интервале, поэтому функция распределения. 2). Если, то. Очевидно случайные события и несовместны, поэтому по формуле сложения вероятностей. По условию событие невозможное и, а. Поэтому. 3). Пусть, тогда. Здесь первое слагаемое, а второе, поскольку событие - невозможное. Таким образом для любого, удовлетворяющего условию. 4). Пусть, тогда. 5). Если, то. 6) При имеем. 7) Если, то. Результаты вычислений представлены на рис. 30.1 графиком функции. В точках разрыва, указана непрерывность функции справа. Основные свойства функции распределения вероятностей Рассмотрим основные свойства функции распределения, следующие непосредственно из определения: 1. Введем обозначение:. Тогда из определения следует. Здесь выражение рассматривается как невозможное событие с нулевой вероятностью. 2. Пусть. Тогда из определения функции следует. Случайное событие является достоверным и его вероятность равна единице. 3. Вероятность случайного события, состоящего в том, что случайная величина принимает значение из интервала при определяется через функцию следующим равенством Для доказательства этого равенства рассмотрим соотношение. События и несовместны, поэтому по формуле сложения вероятностей из (31.3) следует, что и совпадает с формулой (31.2), поскольку и. 4. Функция является неубывающей. Для доказательства рассмотрим. При этом справедливо равенство (31.2). Его левая часть, поскольку вероятность принимает значения из интервала. Поэтому и правая часть равенства (31.2) неотрицательна:, или. Это равенство получено при условии, поэтому - неубывающая функция. 5. Функция непрерывна справа в каждой точке, т.е. где - любая последовательность, стремящаяся к справа, т.е. и. Для доказательства представим функцию в виде: Теперь на основании аксиомы счетной аддитивности вероятности выражение в фигурных скобках равно, таким образом, что и доказывает непрерывность справа функции. Таким образом, каждая функция распределения вероятностей обладает свойствами 1-5. Верно и обратное утверждение: если, удовлетворяет условиям 1-5,то она может рассматриваться как функция распределения некоторой случайной величины. Функция распределения вероятностей дискретной случайной величины Случайная величина называется дискретной, если множество ее значений конечно или счетно. Для полного вероятностного описания дискретной случайной величины, принимающей значения, достаточно задать вероятности того, что случайная величина принимает значение. Если заданы и, тогда функцию распределения вероятностей дискретной случайной величины можно представить в виде: Здесь суммирование ведется по всем индексам, удовлетворяющим условию. Функцию распределения вероятностей дискретной случайной величины иногда представляют через так называемую функцию единичного скачка. При этом принимает вид, если случайная величина принимает конечное множество значений, и верхний предел суммирования в (32.4) полагается равным, если случайная величина принимает счетное множество значений. Пример построения графика функций распределения вероятностей дискретной случайной величины был рассмотрен в п.30. Плотность распределения вероятностей Пусть случайная величина имеет дифференцируемую функцию распределению вероятностей, тогда функция называется плотностью распределения вероятностей (или плотностью вероятности) случайной величины, а случайная величина - непрерывной случайной величиной. Рассмотрим основные свойства плотности вероятности. Из определения производной следует равенство: Согласно свойствам функции имеет место равенство. Поэтому (33.2) принимает вид: Это соотношение объясняет название функции. Действительно, согласно (33.3) функция - это вероятность, приходящаяся на единицу интервала, в точке, поскольку. Таким образом, плотность вероятности, определяемая соотношением (33.3), аналогична определениям плотностей других величин, известных в физике, таких как плотность тока, плотность вещества, плотность заряда и т.д. 2. Поскольку - неубывающая функция, то ее производная - функция неотрицательная: 3. Из (33.1) следует, поскольку. Таким образом, справедливо равенство 4. Поскольку, то из соотношения (33.5) следует Равенство, которое называется условием нормировки. Его левая часть - это вероятность достоверного события. 5. Пусть, тогда из (33.1) следует Это соотношение имеет важное значение для приложений, поскольку позволяет вычислить вероятность через плотность вероятности или через функцию распределения вероятностей. Если положить, то из (33.7) следует соотношение (33.6). На рис. 33.1 представлены примеры графиков функции распределения и плотности вероятностей. Отметим, что плотность распределения вероятности может иметь несколько максимумов. Значение аргумента, при котором плотность имеет максимум называется модой распределения случайной величины. Если плотность имеет более одной моды, то называется многомодальной. Плотность распределения вероятностей дискретной случайной величины распределение дискретный вероятность плотность Пусть случайная величина принимает значения с вероятностями,. Тогда ее функция распределения вероятностей где - функция единичного скачка. Определить плотность вероятности случайной величины по ее функции распределения можно с учетом равенства. Однако при этом возникают математические сложности, связанные с тем, что функция единичного скачка, входящая в (34.1), имеет разрыв первого рода при. Поэтому в точке не существует производная функции. Для преодоления этой сложности вводится -функция. Функцию единичного скачка можно представить через -функцию следующим равенством: Тогда формально производная и плотность вероятности дискретной случайной величины определяется из соотношения (34.1) как производная функции: Функция (34.4) обладает всеми свойствами плотности вероятности. Рассмотрим пример. Пусть дискретная случайная величина принимает значения с вероятностями, и пусть,. Тогда вероятность - того, что случайная величина примет значение из отрезка может быть вычислена, исходя из общих свойств плотности по формуле: Здесь, поскольку особая точка - функции, определяемая условием, находится внутри области интегрирования при, а при особая точка находится вне области интегрирования. Таким образом. Для функции (34.4) также выполняется условие нормировки: Отметим, что в математике запись вида (34.4) считается некорректной (неправильной), а запись (34.2) - корректной. Это обусловлено тем, что -функция при нулевом аргументе, и говорят, что не существует. С другой стороны, в (34.2)-функция содержится под интегралом. При этом правая часть (34.2) - конечная величина для любого, т.е. интеграл от -функции существует. Несмотря на это в физике, технике и других приложениях теории вероятностей часто используется представление плотности в виде (34.4), которое, во-первых, позволяет получать верные результаты, применяя свойства - функции, и во-вторых, имеет очевидную физическую интерпретацию. Примеры плотностей и функций распределения вероятностей 35.1.
Случайная величина называется равномерно распределенной на отрезке, если ее плотность распределения вероятностей где - число, определяемое из условия нормировки: Подстановка (35.1) в (35.2) приводит к равенству, решение которого относительно имеет вид:. Функция распределения вероятностей равномерно распределенной случайной величины может быть найдена по формуле (33.5), определяющей через плотность: На рис. 35.1 представлены графики функций и равномерно распределенной случайной величины. 35.2.
Случайная величина называется нормальной (или гауссовой), если ее плотность распределения вероятностей: где, - числа, называемые параметрами функции. При функция принимает свое максимальное значение:. Параметр имеет смысл эффективной ширины. Кроме этой геометрической интерпретации параметры, имеют и вероятностную трактовку, которая будет рассмотрена в последующем. Из (35.4) следует выражение для функции распределения вероятностей где - функция Лапласа. На рис. 35.2 представлены графики функций и нормальной случайной величины. Для обозначения того, что случайная величина имеет нормальное распределение с параметрами и часто используется запись. 35.3.
Случайная величина имеет плотность распределения вероятностей Коши, если Этой плотности соответствует функция распределения 35.4.
Случайная величина называется распределенной по экспоненциальному закону, если ее плотность распределения вероятностей имеет вид: Определим ее функцию распределения вероятностей. При из (35.8) следует. Если, то 35.5.
Релеевское распределение вероятностей случайной величины определяется плотностью вида Этой плотности соответствует функция распределения вероятностей при и равная при. 35.6.
Рассмотрим примеры построения функции распределения и плотности дискретной случайной величины. Пусть случайная величина - это число успехов в последовательности из независимых испытаний. Тогда случайная величина принимает значения, с вероятностью, которая определяется формулой Бернулли: где, - вероятности успеха и неуспеха в одном опыте. Таким образом, функция распределения вероятностей случайной величины имеет вид где - функция единичного скачка. Отсюда плотность распределения: где - дельта-функция. Сингулярные случайные величины Кроме дискретных и непрерывных случайных величин существуют еще так называемые сингулярные случайные величины. Эти случайные величины характеризуются тем, что их функция распределения вероятностей - непрерывна, но точки роста образуют множество нулевой меры. Точкой роста функции называется значение ее аргумента такое, что производная. Таким образом, почти всюду на области определения функции. Функцию, удовлетворяющую этому условию, также называют сингулярной. Примером сингулярной функции распределения является кривая Кантора (рис. 36.1), которая строится следующим образом. Полагается при и при. Затем интервал разбивается на три равных части (сегмента) и для внутреннего сегмента определяется значение - как полусумма уже определенных значений на ближайших сегментах справа и слева. На данный момент функция определена для, ее значение, и для со значением. Полусумма этих значений равна и определяет значение на внутреннем сегменте. Затем рассматриваются отрезки и, каждый из них разбивается на три равных сегмента и функция определяется на внутренних сегментах как полусумма ближайших справа и слева заданных значений функции. Таким образом, при функция - как полусумма чисел и. Аналогично на интервале функция. Затем функция определяется на интервале, на котором и т.д. Случайные величины. Функция и плотность распределения вероятностей дискретной случайной величины. Сингулярные случайные величины. Математическое ожидание случайной величины. Неравенство Чебышева. Моменты, кумулянты и характеристическая функция. реферат , добавлен 03.12.2007 Понятия теории вероятностей и математической статистики, применение их на практике. Определение случайной величины. Виды и примеры случайных величин. Закон распределения дискретной случайной величины. Законы распределения непрерывной случайной величины. реферат , добавлен 25.10.2015 Вероятность попадания случайной величины Х в заданный интервал. Построение графика функции распределения случайной величины. Определение вероятности того, что наудачу взятое изделие отвечает стандарту. Закон распределения дискретной случайной величины. контрольная работа , добавлен 24.01.2013 Дискретные случайные величины и их распределения. Формула полной вероятности и формула Байеса. Общие свойства математического ожидания. Дисперсия случайной величины. Функция распределения случайной величины. Классическое определение вероятностей. контрольная работа , добавлен 13.12.2010 Функция распределения непрерывной случайной величины. Математическое ожидание непрерывной случайной величины, плотность распределения вероятностей системы. Ковариация. Коэффициент корреляции. лабораторная работа , добавлен 19.08.2002 Особенности функции распределения как самой универсальной характеристики случайной величины. Описание ее свойств, их представление с помощью геометрической интерпретации. Закономерности вычисления вероятности распределения дискретной случайной величины. презентация , добавлен 01.11.2013 Определение вероятностей различных событий по формуле Бернулли. Составление закона распределения дискретной случайной величины, вычисление математического ожидания, дисперсии и среднеквадратического отклонения случайной величины, плотностей вероятности. контрольная работа , добавлен 31.10.2013 Использование формулы Бернулли для нахождения вероятности происхождения события. Построение графика дискретной случайной величины. Математическое ожидание и свойства интегральной функции распределения. Функция распределения непрерывной случайной величины. контрольная работа , добавлен 29.01.2014 Теория вероятностей и закономерности массовых случайных явлений. Неравенство и теорема Чебышева. Числовые характеристики случайной величины. Плотность распределения и преобразование Фурье. Характеристическая функция гауссовской случайной величины. реферат , добавлен 24.01.2011 Вычисление математического ожидания, дисперсии, функции распределения и среднеквадратического отклонения случайной величины. Закон распределения случайной величины. Классическое определение вероятности события. Нахождение плотности распределения. § 1. ПОНЯТИЕ СЛУЧАЙНОЙ ВЕЛИЧИНЫ. В физике и других науках о природе встречается много различных величин разной природы, как например: время, длина, объём, вес и т.д. Постоянной величиной называют ве- личину, принимающую лишь одно фиксированное значение. Величины, которые могут принимать различные значения, на-зываются переменными. Величина считается заданной, если указано множество значений, которые она может принимать. Если однозначно известно, какое именно значение из множества примет величина при создании опреде- лённых условий, то о ней говорят как об «обычной», детерминированной величине. Примером такой величины является количество букв в слове. Большинство физических величин измеряются при помощи приборов с присущей им точностью измерений и, в смысле приведенного определения, они не являются «обычными». Такого рода «необычные» величины называются случайными
. Для случайных величин множество целесообразно назвать множеством возможных значений. Случайная величина принимает то или иное значе- ние с некоторой вероятностью. Заметим, что все величины можно считать случайными, так как детерминированная вели-чина – это случайная величина, принимающая каждое значение с вероятностью, равной единице. Всё сказанное выше является достаточным основанием для изучения случайных величин. Определение. Случайной величиной
называется величина, которая в результате опыта может принимать то или иное (но обязательно только одно) значение, причём заранее, до опыта, неизвестно, какое именно. Понятие случайной величины является фундаментальным понятием теории вероятностей и играет важную роль в её приложениях. Случайные величины обозначаются: , а их зна -чения, соответственно: . Выделяют два основных класса случайных величин: диск -ретные и непрерывные. Определение. Дискретной случайной величиной
называют случайную величину, число возможных значений которой конечное либо счётное множество. Примеры
дискретных случайных величин: 1. - частота попаданий при трёх выстрелах. Возможные значения: 2. - число деффектных изделий из штук. Возможные значения: 3. - число выстрелов до первого попадания. Возможные значения: Определение. Непрерывной случайной величиной
называют такую случайную величину, возможные значения которой не –прерывно заполняют некоторый промежуток (конечный или бесконечный). Примеры
непрерывных случайных величин: 1. - случайное отклонение по дальности от точки попада- ния до цели при выстреле из орудия. Так как снаряд может попасть в любую точку, интервала, ограниченного минимальным и максимальным значениями дальности полёта снаряда, возможных для данного орудия, то возможные значения случайной величины заполняют про -межуток между минимальным и максимальным значением. 2. - ошибки при измерении радиолокатором. 3. - время работы прибора. Случайная величина является своего рода абстрактым вы- ражением некоторого случайного события. С каждым случай -ным событием можно связать одну или несколько характеризу- ющих его случайных величин. Например, при стрельбе по ми -шени можно рассмотреть такие случайные величины: число попаданий в мишень, частота попаданий в мишень, количество очков, набираемых при попадании в определённые области мишени и т.д. § 2 ЗАКОНЫ РАСПРЕДЕЛЕНИЯ ВЕРОЯТНОСТЕЙ СЛУЧАЙНЫХ ВЕЛИЧИН. Определение. Законом распределения случайной величины
называется всякое соотношение, устанавливающее связь меж- ду возможными значениями случайной величины и соответст- вующими им вероятностями. Если вспомнить определение функции, то закон распреде -ления является функцией, область определения которой есть область значений случайной величины, а область значений рассматриваемой функции состоит из вероятностей значений случайной величины. 2.1. РЯД РАСПРЕДЕЛЕНИЯ
Рассмотрим дискретную случайную величину , воз- можные значения которой нам известны. Но зна- ние значений случайной величины, очевидно, не позволяет нам её полностью описать, так как мы не можем сказать, насколь- ко часто следует ожидать тех или иных возможных значений случайной величины при повторении опыта в одних и тех же условиях. Для этого необходимо знать закон распределения вероятностей. В результате опыта дискретная случайная величина прини –мает одно из своих возможных значений, т.е. произойдёт одно из событий: которые образуют полную группу несовместных событий. Вероятности этих событий: Простейшим законом распределения дискретной случайной величины является таблица, в которой приведены все возмож- ные значения случайной величины и соответствующие им ве –роятности: Такую таблицу называют рядом распределения
случайной величины . Для наглядности, ряд распределения можно представить графиком: Эта ломаная называется многоугольником распределения
. Это также одна из форм задания закона распределения дискрет – ной случайной величины . Сумма ординат многоугольника распределения, представля – ющая сумму вероятностей всех возможных значений случай -ной величины, равна единице. Пример 1.
Произведено три выстрела по мишени. Вероят- ность попадания при каждом выстреле равна 0,7. Составить ряд распределения числа попаданий. Случайная величина - «число попаданий» может прин- мать значения от 0 до 3 – х, причём в этом случае вероят – ности определяются по формуле Бернулли: Проверка Пример 2.
В урне назодится 4 белых и 6 чёрных щаров. Наугад извлекаются 4 шара. Найти закон распределения слу- чайной величины - «число белых шаров среди отобран -ных». Эта случайная величина может принимать значения от 0 до 4 – х. Найдём вероятности аозможных значений случайной величины. Можем проверить, что сумма полученных вероятностей рав- на единице. 2.2. ФУНКЦИЯ РАСПРЕДЕЛЕНИЯ
. Ряд распределения нельзя построить для непрерывной слу- чайной величины, так как она принимает бесконечно много значений. Более универсальным законом распределения под- ходящим, как для дискретной, так и для непрерывной слу - чайной величины является функция распределения. Определение. Функцией распределения (интегральным зако- ном распределения) случайной величины называется зада- ние вероятности выполнения неравенства , т.е. Таким образом, функция распределения равна вероят -ности того, что случайная величина в результате опыта попа- дает левее точки . Для дискретной случайной величины, для которой мы знаем ряд распределения: функция распределения будет иметь вид: График функции распределения дискретной случайной вели- чины - разрывная ступенчатая фигура. Для наглядности, рассмотрим пример. Пример 3
Дан ряд паспределения. Найти функцию распре -деления и построить её график По определению, СВОЙСТВА ФУНКЦИИ РАСПРЕДЕЛЕНИЯ 1 Функция распределения - это неотрицательная фун- кция, значения которой заключены между 0 и 1, т.е. 2 Вероятность появления случайной величины в про- межутке равна разности значений функции распределения на концах промежутка: 3 Функция распределения - неубывающая функция, т.е. при выполнено: ; Перейдём в равенстве (2) к пределу при . Полу- чим вместо вероятности попадания случайной величины в про- межуток вероятность точечного значения случайной величины, т.е. Значение этого предела зависит от того, является ли точка точкой непрерывности функции , или в этой точке функция имеет разрыв. Если функция непрерыв- на в точка , то предел равен 0, т.е. . Если же в этой точке функция имеет разрыв (1 – го ро- да), то предел равен значению скачка функции в точке . Так как непрерывная случайная величина имеет непрерыв -ную функцию распределения , то из равенства нулю предела (3) следует, что вероятность любого фиксированного значения непрерывной случайной величины равна нулю. Это следует из того, что возможных значений непрерывной случайной величины бесконечно много. Из этого, в частности, следует, что следующие вероятности совпадают: Приведённые свойства функции распределения можно сфор- мулировать следующим образом: функция распределения - это неотрицательная неубывающая функция, удовлетворяющая ус –ловиям: Обратное утверждение также имеет место: монотонно возрастающая непрерывная функция, удовлетворяющая условиям является функцией распределения некоторой непрерывной слу- чайной величины. Если значения этой величины сосредоточе -ны на некотором промежутке , то график этой функции можно схематически изобразить следующим образом: Рассмотрим пример.
Функция распределения непрерывной случайной величины задана следующим образом: Найти значение « », построить график и найти веро –ятность Так как функция распределения непрерывной случайной ве- личины непрерывна, то - непрерывная функция, и при должно выполгяться равенство: Построим график этой функции Найдём требуемую вероятность Замечание.
Функцию распределения, иногда ещё называют интегральным законом распределения
. Ниже объясним, почему именно. 2.3 ПЛОТНОСТЬ РАСПРЕДЕЛЕНИЯ.
Так как с помощью функции распределения дискретной случайной величины в любой точке мы можем определить вероятность возможных значений, то она однозначно опре- деляет закон распределения дискретной случайной величины. Однако по функции распределения трудно судить о харак- тере распределения непрерывной случайной величины в не -большой окрестности той или иной точки числовой оси. Более наглядное представление о характере распределения непрерывной случайной величины вблизи различных точек даёт функция, которую называют плотностью распределения (или дифференциальным законом распределения)
Пусть - непрерывная случайная величина с функцикй распределения . Найдём вероятность попадания этой случайной величины в элементарный участок . По формуле (2), имеем Разделим это равенство на Отношение, стоящее слева, называется средней вероятно –стью
на единице длины участка. Считая функцию дифференцируемой, перейдём к перейдём в этом равенстве к пределу Определение.
Предел отношения вероятности попадания непрерывной случайной величины на элементарный участок к длине этого участка при называ- ется плотностью распределения
непрерывной случайной ве – личины и обозначается Следовательно, Плотность распределения показывает, насколько часто слу -чайная величина появляется в некоторой окрестности точ –ки при повторении опытов. Кривая, изображающая график плотности распределения, на- зывается кривой распрелеления.
Если возможные значения случайной величины запол- няют некоторый промежуток , то вне этого промежутка. Определение.
Случайная величина называется непре – рывной
, если её функция распределения непрерывна на всей числовой прямой, а плотность распределения не- прерывна везде, за исключением может быть конечного числа точек (точек разрыва 1 – го рода). СВОЙСТВА ПЛОТНОСТИ РАСПРЕДЕЛЕНИЯ 1. Плотность распределения неотрицательна, т.е. (это следует из того, что - производная неубывающей функции ). 2. Функция распределения непрерывной случайной величи- ны равна интегралу от плотности распределения (и поэтому является интегральным законом распределения), т.е. В самом деле, (по определению дифференциала функции). Следовательно, На графике плотности распределения функция распределения изображается площадью заштрихованной области. 3. Вероятность попадания случайной величины на участок равна интегралу от плотности распределения по этому промежутку, т.е. В самом деле, 4. Интеграл в бесконечных пределах от плотности распре –деления равен единице, т.е. Другими словами, площадь фигуры под графиком плотности распределения равна 1. В частности, если возможные значе- ния случайной величины сосредоточены на участке , то Пример.
Пусть плотность распределения зазана функцией Найти: а) значение параметра ; б) функцию распределения в) Вычислить вероятность того, что случайная величи- на примет значение из отрезка . а) По свойству 4, . Тогда б) По свойству 2, Если , Таким образом, в) По свойству 3, § 3. ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ СЛУЧАЙНЫХ При решении многих практических задач нет необходимости знать все вероятностные характеристики случайной величины. Иногда достаточно знать только некоторые числовые характе - ристики закона распределения. Числовые характеристики позволяют в сжатой форме выра -зить наиболее существенные особенности того или иного рас- пределения. О каждой случайной величине прежде всего необходимо знать её среднее значения, около которого группируются все возможные значения этой величины, а также некоторое число, характеризующее степень рассеяния этих значений относитель- но среднего. Различают характеристики положения и характеристики рас- сеяния. Одной из самых важных характеристик положения яв- ляется математическое ожидание. 3.1 Математическое ожидание (среднее значение).
Рассмотрим сначала дискретную случайную величину, име -ющую возможные значения с вероятностями Определение. Математическим ожиданием
дискретной слу- чайной величины называется сумма произведений всех возможных значений этой величины на их вероятности, т.е. По другому, математическое ожидание обозначается Пример.
Пусть дан ряд распределения: Рассмотрим теперь непрерывную случайную величину все возможные значения которой заключены в отрезке . Разобьём этот отрезок на частичных отрезков, длины которых обозначим: Так как произведение при- ближённо равно вероятности попадания случайной величины на элементарный участок , то сумма произведений Тогда Определение. Математическим ожиданием
непрерывной случайной величины называется следующий определённый интеграл: Если непрерывная случайная величина принимает значения на всей числовой прямой, то Пример.
Пусть дана плотность распределения непрерывной случайной величины: Тогда её математическое ожидание: Понятие математического ожидания имеет простую меха -ническую интерпретацию. Распределение вероятностей слу -чайной величины можно интерпретироварь как распределение единичной массы по прямой. Дискретной случайной величине, принимающей значения с вероятностями соответствует прямая, на которой массы сосредоточены в точках . Непре- рывной случайной величине отвечает непрерывное распреде -ление масс на всей прямой или на конечном отрезке этой прямой. Тогда математическое ожидание - это абсцисса цент- ра тяжести
. СВОЙСТВА МАТЕМАТИЧЕСКОГО ОЖИДАНИЯ 1. Математическое ожидание постоянной величины равно самой постоянной: 2. Постоянный множитель можно вынести за знак матема- тического ожидания: 3. Математическое ожидание алгебраической суммы слу –чайных величин равна алгебраической сумме их мате- матических ожиданий: 4. Математическое ожидание произведения независимых случайных величин равно произведению их математи -ческих ожиданий: 5. Математическое ожидание отклонения случайной вели- чины от её математического ожидания равно нулю: 3.2. Мода и медиана случайной величины.
Это ещё две характеристики положения случайной вели- чины. Определение. Модой
дискретной случайной величины называется её наиболее вероятное значение. Для непрерыв –ной случайной величины мода - это точка максимума функ- ции . Если многоугольник распределения (для дискретной случай- ной величины) или кривая распределение (для непрерывной случайной величины) имеет две или более точек максимума, то распределение называется двухмодальным или многомо -дальным, соответственно. Если нет ни одной точки максимума, то распределение называется антимодальным. Определение. Медианой
случайной величины на – зывается такое её значение, относитеоьно которого равноверо- ятны получение большего или меньшего значения случайной величины, т.е. Другими словами, - это абсцисса точки, в которой площадь под графиком плотности распределения (многоуголь- ником распределения) делится пополам. Пример.
Дана плотность случайной величины: Найти медиану этой случайной величины. Медиану найдём из условия Из четырёх корней необходимо выбрать тот, который заключён между 0 и 2, т.е. Замечание
. Если распределение случайной величины одно- модальное и симметричное (нормальное), то все три характе -ристики положения: математическое ожидание, мода и медиа -на, совпадают. 3.3 Дисперсия и среднее квадратическое отклонение.
Значения наблюдаемых случайных величин, обычно, более или менее колеблются около некоторого среднего значения. Это явление называется рассеянием случайной величины око- ло её среднего значения. Числовые характеристики, показыва- ющие, насколько плотно сгруппированы возможные значения случайной велипины около среднего, называются характерис – тиками рассеяния. Из свойства 5 математического ожидания следует, что линейное отклонение значений случайной вели –чины от среднего значения не может служить характеристикой рассеяния, так как положительные и отрицательные отклоне –ния «гасят» друг друга. Поэтому основной характеристикой рассеяния случайной величины принято считать математичес - кое ожидание квадрата отклонения случайной величины от среднего. Определение. Дисперсией
называется математическое ожи –дание квадрата отклонения случайной величины от её матема- тического ожидания (среднего значения), т.е. Но, несмотря на удобства этой характеричтики рассеяния, желательно иметь характеристику рассеяния соразмерную с самой случайной величиной и её математическим ожиданием. Поэтому вводится ещё одна характеристика рассеяния, кото -рая называется средним квадратическим отклонением
и рав -на корню из дисперсии, т.е. . Для вычисления дисперсии удобно пользоваться формулой, которую даёт следующая теорема. ТЕОРЕМА.
Дисперсия случайной величины равна разности между математическим ожиданием квадрата случайной вели -чины и квадратом её математического ожиданием, т.е. В самом деле, по определению Так как . СВОЙСТВА ДИСПЕРСИИ: 1. Дисперсия постоянной случайной величины равна нулю, т.е. 2. Постоянный множитель сучайной величины выносится из дисперсии с квадратом, т.е. 3. Дисперсия алгебраической суммы двух случайных вели- чин равна сумме их дисперсий, т.е. Следствие
из 2 и 3 свойств: Рассмотрим примеры.. Пример 1.
Дан ряд распределения дискретной случайной величины. Найти её среднее квадратическое отклонение. Сначала найдём Тогда среднее квадратическое отклонение Пример 2
. Пусть дана плотность распределения непрерыв -ной случайной величины: Найти её дисперсию и среднее квадратическое отклонение. 3.4 Моменты случайных величин.
Различают моменты двух видов: начальные и центральные. Определение. Начальным моментом порядка
случайной величины называют математическое ожидание величины , т.е. . Для дискретной случайной величины: Для непрерывной случайной величины: В частности, математическое ожидание - это началь- ный момент 1 – го порядка. Определение. Центральным моментом полрядка
слу -чайной величины называется математическое ожидание ве- личины , т.е. Для дискретной случайной величины: Для непрерывной - Центральный момент 1 – го порядка равен нулю (свойство 5 математического ожидания); ; характеризует асимметрию (скощенность) графика плотности распределения. называется коэффициентом асимметрии.
Служит для характеристики островерхости распределения. Определение. Эксцессом
случайной величины называет- ся число Для номально распределённой случайной величины отноше- ние . Поэтому кривые распределения, более островер- хие, чем нормальная, имеют положительный эксцесс (), а более плосковерхие имеют отрицательный эксцесс (). Пример.
Пусть дана плотность распределения случайной величины : Найти коэффициент асимметрии и эксцесс этой случайной величины. Найдём необходимые для этого моменты:
Подобные документы
СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
![]()
![]()

![]() .
.![]()
0,027
0,189
0,441
0,343
![]() (1)
(1)
![]()
0,2
0,1
0,3
0,4




![]() или , т.е.
или , т.е.


![]()

![]()



![]() Если
Если ![]() .
.
0,2
0,1
0,3
0,4
![]() , и в каждом частичном интервале возьмём по произвольной точке, соответственно .
, и в каждом частичном интервале возьмём по произвольной точке, соответственно .![]() составленная по аналогии с опреде -лением математического ожидания дискретной случайной ве- личины, приближённо равна математическому ожиданию не -прерывной случайной величины Пусть .
составленная по аналогии с опреде -лением математического ожидания дискретной случайной ве- личины, приближённо равна математическому ожиданию не -прерывной случайной величины Пусть .![]()
![]() (2)
(2)![]()


![]()

![]() . В нашем случае,
. В нашем случае,
![]()
![]() (3)
(3)![]() (4) для непрерывной случайной величины:
(4) для непрерывной случайной величины:![]() (5)
(5)![]()
![]()
![]()
- 1
0,2
0,05
0,2
0,3
0,25




![]()
![]()
![]()
![]()





 Тогда коэффициент асимметрии:
Тогда коэффициент асимметрии: ![]() (отрицательная асимметрия).
(отрицательная асимметрия).